Introdução
Na v1.24, Go substituiu sua implementação de Map por uma nova versão de tabela hash chamada Swiss Table, ou flat_hash_map.
O que é uma Swiss Table? Uma Swiss Table é um map que usa uma abordagem cache-friendly e mais eficiente (com menor footprint de memória) que torna as comparações e inserções mais rápidas.
Também usa uma estratégia diferente para lidar com colisões: linear probing on steroids ao invés da estratégia anterior de chaining.
Ao trabalhar com hash-tables, uma coisa é certa: haverá conflito.

O Antigo Map
A implementação anterior era altamente otimizada para eficiência de memória e desempenho.
A equipe Go é incrível.
Encadeamento
Como funciona? Pré-aloca memória na forma de buckets, onde cada bucket pode ter até 8 pares key-value. Quando um bucket está cheio (ou meio cheio), o algoritmo aloca um novo overflow bucket como uma lista encadeada, em um processo conhecido como chaining.
À medida que a tabela se aproxima de uma alta taxa de fator de carga*, o runtime move todas as entradas para um novo bloco de endereço de memória (geralmente duas vezes maior que o anterior), isso é conhecido como rehashing.
* Fator de Carga = posições usadas / capacidade total
No encadeamento tradicional, sempre que há um conflito, o runtime aloca memória para um novo node/par key-value e o armazena como uma lista encadeada.
Vou focar em como o chaining funciona para nodes e deixar a explicação da estratégia de buckets para a Implementação do Map no Go 1.23.
Exemplo Prático
Imagine uma função hash que, baseada em uma string, retorna um índice (valor de offset) para um endereço de memória fixo:
x = len(x)
Geralmente, essas funções tentam produzir um efeito avalanche para distribuir os resultados "uniformemente" sobre o intervalo de memória do map.
Nossa função de hashing é mais vulnerável a conflitos, pois apenas retorna o tamanho da string para definir o endereço.
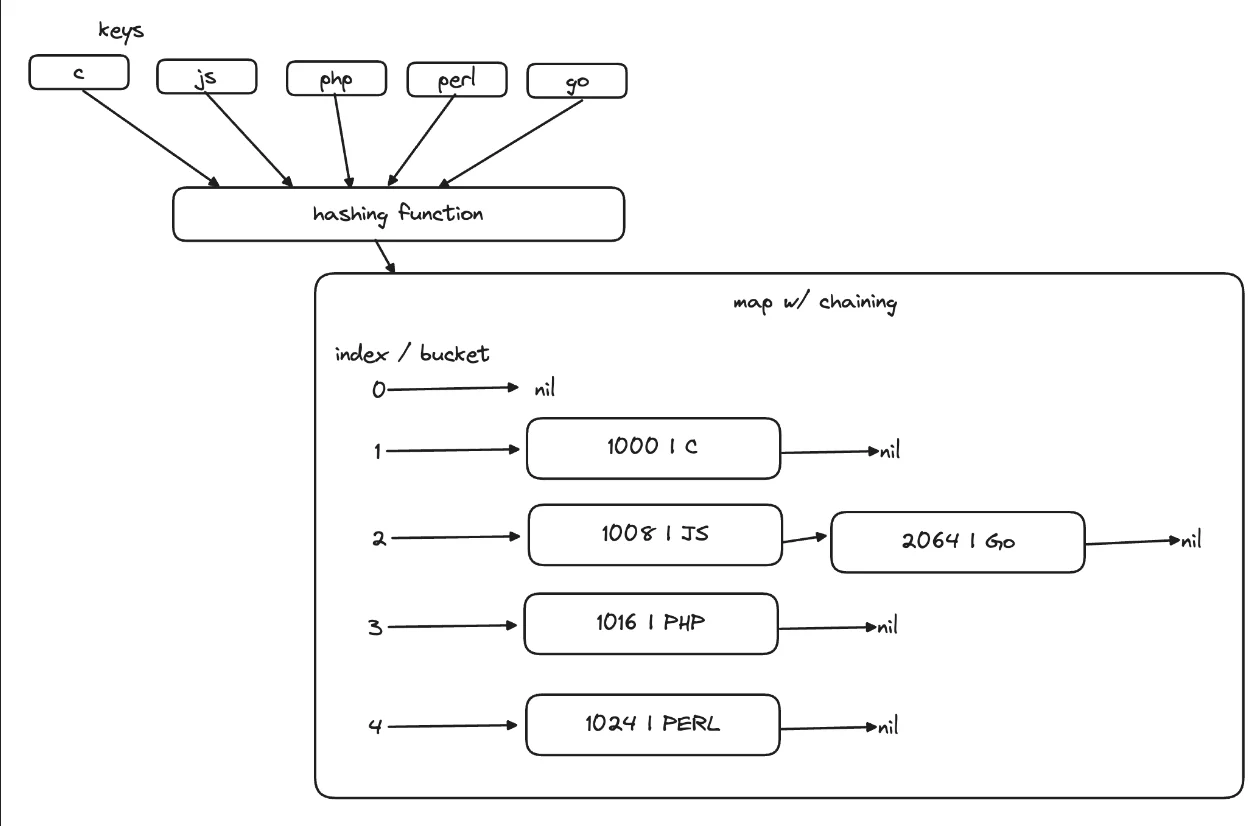
Agora, vamos supor que adicionamos as seguintes chaves:
| key | index |
|---|---|
| C | 1 |
| JS | 2 |
| PHP | 3 |
E esta tabela:
| index | key | memory | next |
|---|---|---|---|
| 0 | nil | 0 | nil |
| 1 | C | 1000 | nil |
| 2 | JS | 1008 | nil |
| 3 | PHP | 1016 | nil |
| 4 | PERL | 1024 | nil |
Quando adicionamos uma nova chave "Go", causamos um conflito.
Como o índice de "Go" é 2 e já existe "JS" na posição 2, a estratégia alocará um novo node na memória disponível e apontará a propriedade next de "JS" para "Go".
| index | key | memory | next |
|---|---|---|---|
| 0 | nil | 0 | nil |
| 1 | C | 1000 | nil |
| 2 | JS | 1008 | 2064 |
| 3 | PHP | 1016 | nil |
| 4 | PERL | 1024 | nil |
| __ | Go | 2064 | nil |
Então temos chaves, que são usadas como entradas em uma função hash, que gera um índice (ou um offset para um endereço de memória fixo/início da lista) e as chaves ou nodes ou buckets são inseridos como listas encadeadas.
Problema
Como você pode ver, cada novo node é colocado longe de sua chave de conflito na memória.
Isso significa que, ao procurar por uma chave que tem conflitos (Go, por exemplo), o processador buscará endereços esparsos na memória.
Embora a implementação anterior do Go usasse muitas técnicas de melhoria de desempenho (como usar buckets de 8 tamanhos em vez de single-nodes) e comparando parcialmente as chaves (7 bits em vez de 64), esta abordagem de encadeamento não é cache-friendly.
Você pode verificar os detalhes específicos aqui.
Swiss Table
É uma implementação inteligente que usa metadata de 1 byte e linear probing turbinado.
Linear Probing
Não mais alocação dinâmica de memória para buckets com listas encadeadas.
Considere esta tabela:
| index | key | memory |
|---|---|---|
| 0 | nil | 1000 |
| 1 | C | 1008 |
| 2 | JS | 1016 |
| 3 | PHP | 1024 |
| 4 | PERL | 1032 |
| 5 | nil | 1040 |
| ... | ... | ... |
| N | nil | N_ADDRESS |
| Uma melhor visualização neste caso é olhar para a tabela hash como um, bem, _flat_hash_map. |
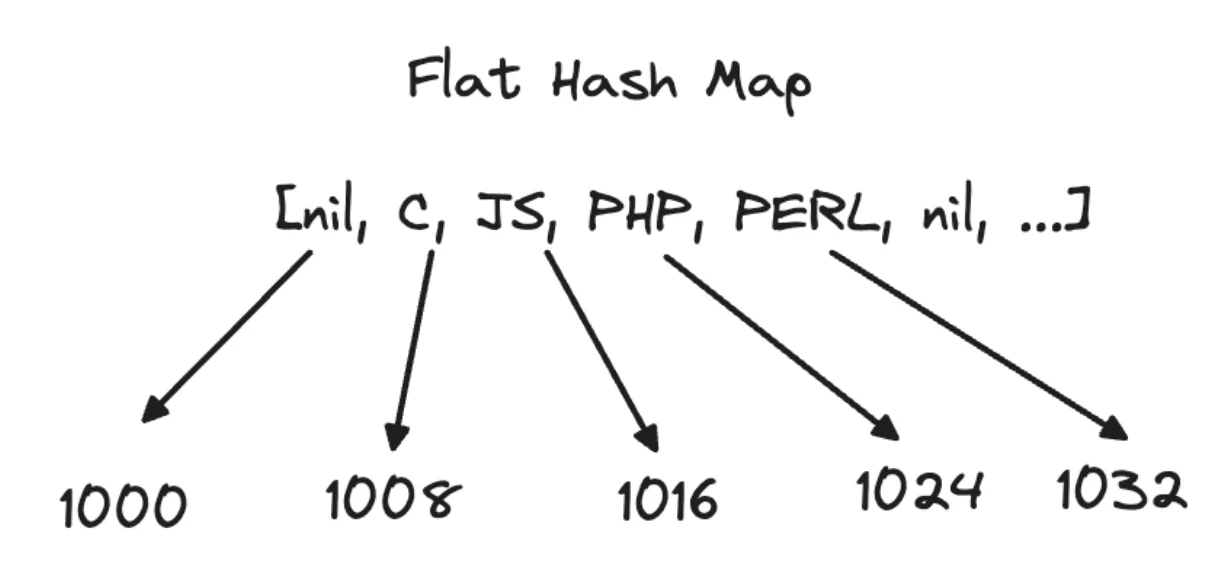
Quando ocorre um conflito, o algoritmo buscará linearmente pela próxima posição, uma por uma.
Para adicionar "Go", temos:
- hash("Go") = 2
- Vê o slot 1016 e percebe que está preenchido.
- Vê o slot 1024 e percebe que está preenchido.
- Vê o slot 1032 e percebe que está preenchido.
- Slot 1040 está aberto, use-o.
É apenas no slot 1040 que encontrará um espaço aberto, é aqui que a chave "Go" vai.
O importante a notar é que desta vez, as colisões estão localizadas próximas umas das outras, tornando-as cache friendly, o que acelera um pouco as coisas.
Esteroides (SSE3)
Streaming SIMD Extensions 3 é um tipo de instrução de processador que, combinada com técnicas curadas de engenharia de software como manipulação de bits, fornece uma maneira de realizar leituras paralelas de endereços de memória com uma única instrução.
O que significa que, ao sondar colisões, a Swiss Table pode realizar até 16 verificações de uma vez, embora o Golang pareça estar usando apenas 8, é muito melhor do que verificar uma por uma!
Metadata
Swiss Table usa um byte de metadata para armazenar parcialmente a chave hasheada, permitindo comparação rápida (7 bits em vez de 64).
Com linear probing (também conhecido como open addressing) + metadata chunking + SSE3, comparações e inserções são mais rápidas e consomem menos memória do que a implementação anterior.
1.23.4 vs 1.24
Executei o script de benchmark deste artigo no meu laptop.
O teste foi:
- Criar e popular um map de
1_000_000itens - Realizar
10_000_000lookups usando indexação mod. - Inserir
1_000_000novas entradas no map. - Remover os primeiros
1_000_000do map.
Resultados
| Operação | Go 1.23 (ms) | Go 1.24 (ms) | Melhoria (%) |
|---|---|---|---|
| Lookup | 287.340375 | 184.787167 | 35.67% mais rápido |
| Inserção | 118.564333 | 66.4095 | 43.99% mais rápido |
| Deleção | 39.893875 | 61.364875 | -53.85% mais lento |
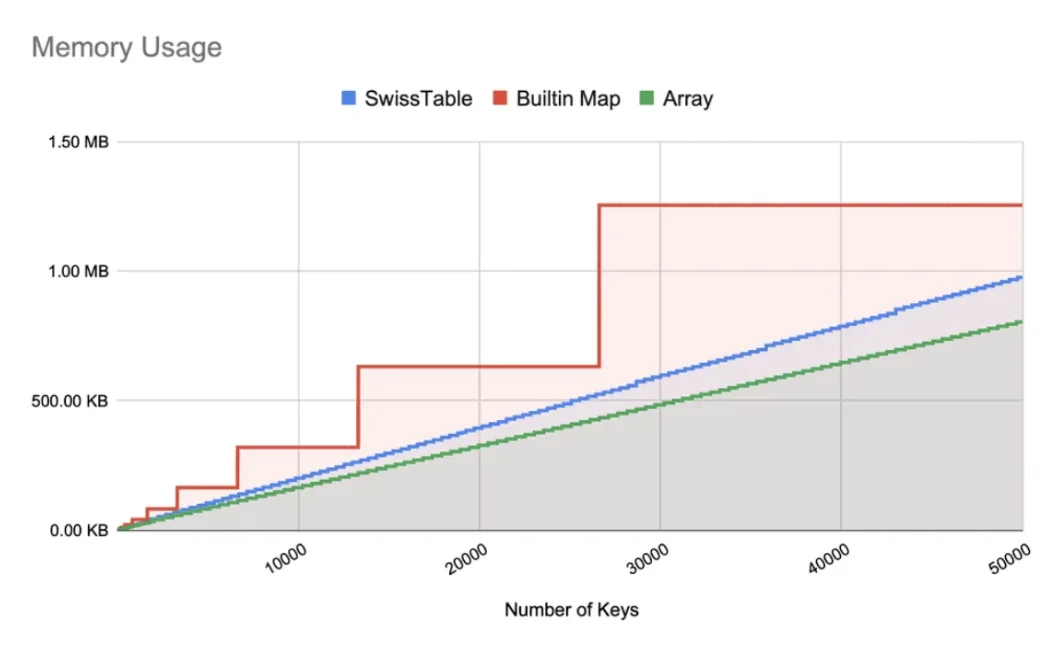
No artigo Go 1.24's Swiss Tables: The Silver Bullet or Just a Shiny New Gadget?, também podemos ver a eficiência das Swiss Tables no uso de memória.
Problema
Embora a Go Swiss Table use buckets e uma função hash esparsa (para o efeito avalanche) para distribuir as chaves uniformemente sobre o bloco de memória pré-alocado, à medida que a tabela fica cheia, os conflitos gerarão seções clusterizadas que aumentarão o tempo de busca.
É fácil ver isso acontecendo com uma tabela de 10 posições:
Table: [nil, C, JS, PHP, PERL, nil, nil, nil, nil, nil]
Adicionar uma nova chave "B" causaria:
- len(B) = 1
- posição 1 está ocupada por "C", olhe a próxima
- posição 2 está ocupada por "JS", olhe a próxima
- posição 3 está ocupada por "PHP", olhe a próxima
- posição 4 está ocupada por "PRL", olhe a próxima
- posição 4 está livre, adicione "B"
Table: [nil, C, JS, PHP, PERL, B, nil, nil, nil, nil]
Index: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Agora, qualquer chamada de função hash que retornasse 1, 2, 3, 4 ou 5 exigiria buscar até 4 posições, moleza para o SSE3, eu reconheço, mas e se houvesse uma maneira melhor?
Elastic Hashing
Em janeiro de 2025, um novo paper sobre open addressing foi lançado sugerindo uma nova abordagem, teoricamente melhor do que linear probing, chamada Elastic Hashing.
Sinta-se livre para ler o artigo de notícia ou o paper para obter o contexto completo.
Afirma superar uma conjectura de 40 anos (conjectura de Yao), que defende o linear probing como simples, com eficiência quase ótima, que não se degrada catastroficamente à medida que a carga aumenta.
Krapivin descobriu a nova estratégia sem estar ciente da conjectura de Yao, o que indica que devemos desafiar restrições conhecidas com mais frequência.
O que é?
Basicamente, em vez de verificar posições uma por uma, ou 16 por 16 (como nossas amadas Swiss Tables fazem), criou uma nova estratégia bidimensional para calcular o endereço de inserção usando virtual overflow buckets.
A ideia é que existe uma nova função chamada φ(i, j) que retorna uma posição de um node, onde:
- i = Bucket Primário (Resultado do Hash)
- j = Contagem de Overflow
Então, usando nossa função hash anterior, ambas as chaves "JS" e "Go" retornariam 2 como seu "Bucket Primário".
A ordem de inserção determinaria se a chave seria colocada na posição φ(2, 1) = 2 ou talvez φ(2, 2) = 7.
Mágica
A mágica está na função φ, que é capaz de criar virtualmente buckets de overflow para colisões_. Supera a complexidade do algoritmo para linear probing nos piores e casos médios, com esses saltos ou buracos de minhoca, sonda menos endereços, levando a um melhor desempenho teórico de inserção.

Elastic Hashing será aplicado às Swiss Tables? Talvez. Espero que sim. O tempo dirá.
Ainda tenho perguntas em aberto:
- O elastic hashing provará ser mais rápido do que linear probing + SSE3?
- O Elastic Hash pode se beneficiar das leituras paralelas do SIMD?
- Qual linguagem será a primeira a implementar este novo algoritmo?
Se você, por acaso, cruzar com algumas dessas respostas por aí, deixe um comentário!
Conclusão
É bom experimentar essas últimas melhorias na eficiência de Hash Table à medida que acontecem, em tempo real.
Um paper de um mês de idade melhorando a complexidade do código de um aspecto do algoritmo da estrutura de dados central é uma ótima notícia!
Mostra que não há limites para melhorias de desempenho, nem mesmo regras de décadas estão seguras, não importa onde você esteja, sempre há espaço para melhorias.
Saúde.
Referências
- Maps are faster in Go 1.24 - Matt Boyle
- # Go 1.24's Swiss Tables: The Silver Bullet or Just a Shiny New Gadget? - David Lee
- Undergraduate upends a 40 year old data science conjecture - Quanta Magazine
- Optimal Bounds for Open Addressing Without Reordering - Martin Farach-Colton, Andrew Kapivin, William Kuszmaul